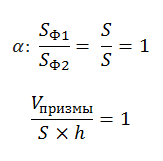что значит измерить объем фигуры
ВОПРОСЫ
1. Какими свойствами обладает объем фигуры?
1) Равные фигуры имеют равные объемы.
2) Объем фигуры равен сумме объемов фигур, из которых она состоит.
2. Какой куб называют единичным?
3. Приведите примеры единиц измерения объема.
4. Что означает измерить объем фигуры?
5. Чему равен объем прямоугольного параллелепипеда с измерениями а, b, c?
6. По какой формуле вычисляется объем куба?
7. Как вычислить объем прямоугольного параллелепипеда, зная его площадь основания и высоту?
РЕШАЕМ УСТНО
1. Заполните пропуски в цепочки вычислений:
2. Сколько необходимо использовать кубиков с ребром 1 см, сложить кубик с ребром 2 см?
Нужно взять 8 кубиков с ребром 1 см.
3. Сколько сантиметров проволоки необходимо для изготовления проволочного каркаса прямоугольного параллелепипеда, измерения которого равны 3 см, 5 см и 6 см?
УПРАЖНЕНИЯ
617. 1) Сколько сантиметров в одном дециметре? Квадратных сантиметров в одном квадратном дециметре? Кубических сантиметров в одном кубическом дециметре?
2) Сколько сантиметров в одном метре? Квадратных сантиметров в одном квадратном метре? Кубических сантиметров в одном кубическом метре?
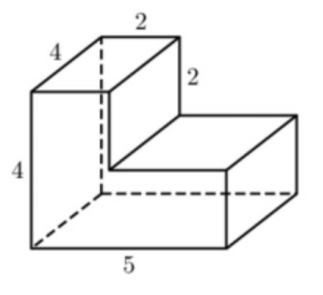
618. Фигуры, изображенные на рисунке 179, сложены из кубиков, ребра которых равны 1 см. Найдите объем каждой фигуры.
619. Вычислите объем прямоугольного параллелепипеда, измерения которого равны 12 м, 15 м и 6 м.
620. Чему равен объем куба, ребро которого равно 6 см?
621. Чему равен объем прямоугольного параллелепипеда с измерениями 10 дм, 8 дм и 4 дм?
622. Выразите:
1) в кубических миллиметрах: 7 см3, 38 см3; 12 см3 243 мм3; 42 см3 68 мм3; 54 см3 4 мм3; 1 дм3 20 мм3; 18 дм3 172 см3; 35 дм3 67 см3 96 мм3;
2) в кубических дециметрах: 4 м3; 264 м3; 10 м3 857 дм3; 28 м3 2 дм3; 44 000 см3; 5 430 000 см3.
623. Выразите в кубических сантиметрах: 8 дм3; 62 дм3; 378 000 мм3; 520 000 мм3; 78 дм3 325 см3; 56 дм3 14 см3; 8 м3 4 дм3 6 см3.
625. Высота прямоугольного параллелепипеда равна 20 см, что на 4 см меньше его длины и в 5 раз больше его ширины. Вычислите объем данного параллелепипеда.
629. Спортивный зал имеет форму прямоугольного параллелепипеда, его объем равен 960 м3, а площадь пола равна 192 м2. Найдите высоту спортивного зала.
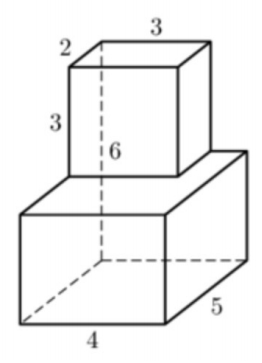
630. Найдите объем фигуры, изображенной на рисунке 180 (размеры даны в сантиметрах).
631. Найдите объем фигуры, изображенной на рисунке 181 (размеры даны в сантиметрах).
632. Ребро куба, изготовленного из цинка, равно 4 см. Найдите массу куба, если 1 см3 цинка составляет 7 г.
633. Знайка сконструировал землеройную машину, которая за 8 ч может вырыть траншею, имеющую форму прямоугольного параллелепипеда, длиной 150 м, глубиной 80 см и шириной 60 см. Сколько кубометров земли выкапывает эта машина за 1 ч? Работу скольких коротышек выполняет эта машина, если за 8 ч один коротышка может выкопать 240 дм3 земли?
634. Куб и прямоугольный параллелепипед имеют равные объемы. Найдите площади поверхности куба, если длина прямоугольного параллелепипеда равна 12 см, что в 2 раза больше ширины и в 4 раза больше высоты параллелепипеда.
635. Ребро одного куба в 4 раза больше ребра второго. Во сколько раз: 1) площадь поверхности первого куба больше площади поверхности второго; 2) объем первого куба больше объема второго?
638. В бассейн, площадь которого равна 1 га, налили 1 000 000 л воды. Можно ли в этом бассейне провести соревнования по плаванию?
639. В кубе с ребром 3 см проделали три сквозных квадратных отверстия со стороной 1 см (рис. 182). Найдите объем оставшейся части.
640. Размеры куска мыла, имеющего форму прямоугольного параллелепипеда, равны 12 см, 6 см и 4 см. Каждый день используют одинаковую массу мыла. Через 14 дней все размеры куска мыла уменьшились в 2 раза. На сколько дней хватит оставшегося куска мыла?
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
642. Из двух населенных пунктов, расстояние между которыми равно 54 км, одновременно выехали навстречу друг другу и встретились через 2 ч после начала движения. Скорость движения первого велосипедиста составляла 12 км/ч. С какой скоростью двигался второй велосипедист?
643. Найдите значение выражения:
ЗАДАЧА ОТ МУДРОЙ СОВЫ
Объемы геометрических тел
Объемы геометрических тел
Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров «Российского учебника» учитель высшей категории Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.
Определение объема
Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:
Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.
В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.
Примеры
Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
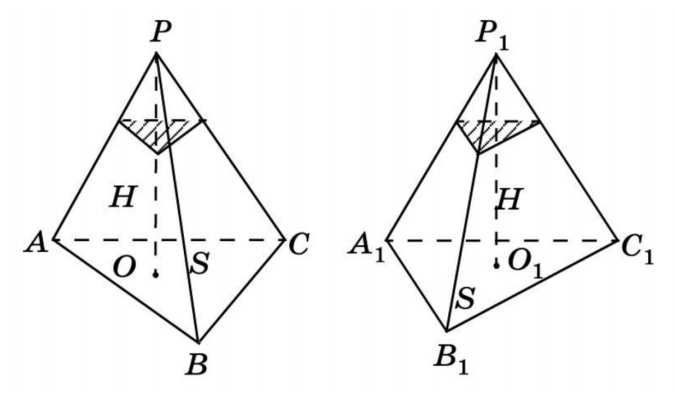
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Разберем, как можно вычислять объемы изучаемых в школе фигур.
Объем призмы
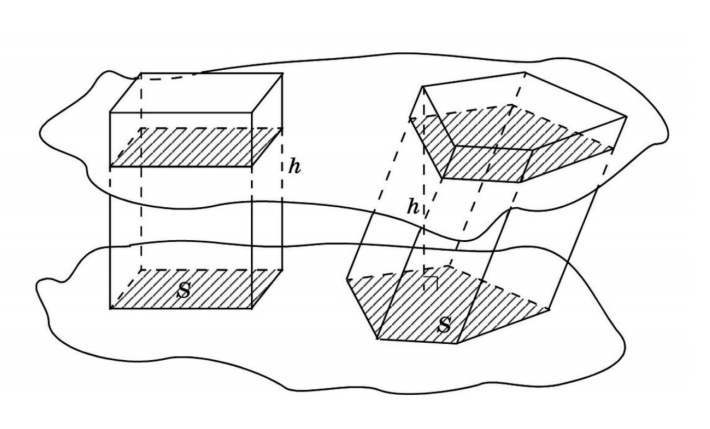
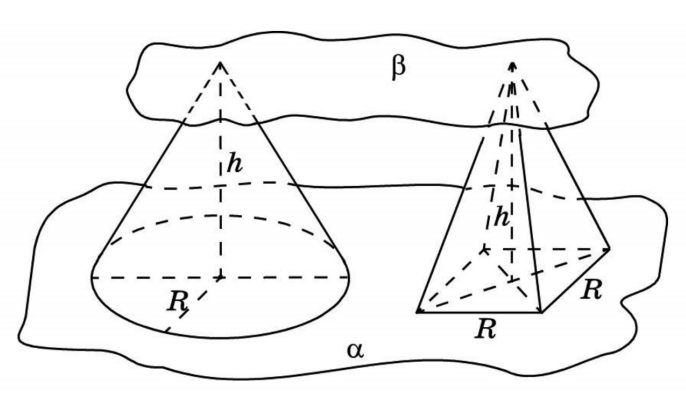
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф2) поместим прямоугольный параллелепипед (Ф1), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:
Объем пирамиды
Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.
Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.
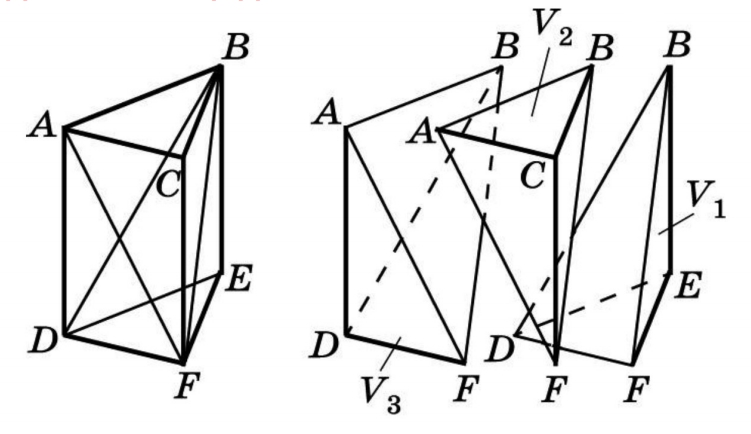
Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:
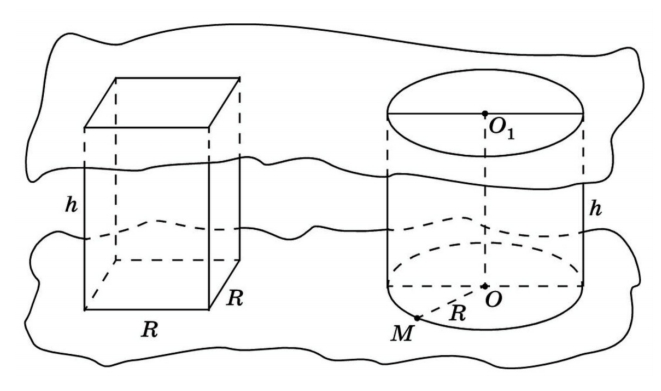
Объем цилиндра
Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:
Объем конуса
Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.
Объем шара
Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.
Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.
Объем прямоугольного параллелепипеда
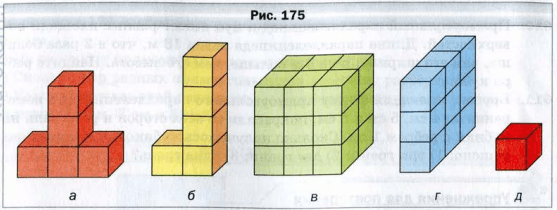
Фигуры на рисунке 175, а и б состоят из равного количества одинаковых кубиков. О таких фигурах можно сказать, что их объемы равны. Прямоугольные параллелепипеды, изображенные на рисунке 175, в и г, состоят соответственно из 18 и 9 одинаковых кубиков. Поэтому можно сказать, что объем первого из них в два раза больше объема второго.
С такой величиной, как объем, вы часто встречаетесь в повседневной жизни: объем топливного бака, объем бассейна, объем классной комнаты, показатели потребления газа или воды на счетчиках и т.д.
Опыт подсказывает вам, что одинаковые емкости имеют равные объемы. Например, одинаковые бочки имеют равные объемы.
Если емкость разделить на несколько частей, то объем всей емкости равен сумме объемов ее частей. Например, объем двухкамерного холодильника равен сумме объемов его камер.
Эти примеры иллюстрируют следующие свойства объема фигуры.
1 ) Равные фигуры имеют равные объемы.
2 ) Объем фигуры равен сумме объемов фигур, из которых она состоит.
Как и в случаях с другими величинами (длина, площадь), следует ввести единицу измерения объема.
За единицу измерения объема выбираю куб, ребро которого равно единичному отрезку. Такой куб называют единичным.
Измерить объем фигуры − значит подсчитать, сколько единичных кубов в ней помещается.
Если объем красного кубика (см. рис. 175, д) принять за единицу, то объемы фигур на рисунке 175, а, б, в и г соответственно равны 5, 5, 18 и 9 кубических единиц.
Объем прямоугольного параллелепипеда равен произведению трех его измерений.
V = abc
Поскольку у куба все ребра равны, то его объем вычисляют по формуле:
V = a 3
где a − длина ребра куба. Именно поэтому третью степень числа называют кубом числа.
Итак, мы получили еще одну формулу для вычисления объема прямоугольного параллелепипеда:
V = Sh
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
Решение. Из формулы V = Sh следует, что h = V : S. Тогда искомую высоту h бака можно вычислить так:
Как измерить талию и не ошибиться с результатом: 5 простых шагов
Пошаговая инструкция, как правильно измерить талию, реальные показатели талии здоровых людей, и почему не стоит переживать, если ваши объемы больше, чем у других – отвечаем в тексте на самые частые вопросы о замерах одной из самых популярных частей тела. А еще делимся упражнением для уменьшения талии.
Для худеющих людей замеры частей тела – неотъемлемая часть приведения в порядок фигуры. Именно поэтому так важно понимать, как именно можно измерить обхват талии, да еще и сделать это правильно. Информация о том, какого размера ваша талия, необходима еще и тогда, когда вы выбираете себе одежду, ведь многие производители уточняют размер в сантиметрах, чтобы покупатель понимал, подойдет ему та или иная блузка или нет. Кроме того, по измерениям объема талии можно понять, здоровы ли вы. Рассказываем, как измерить талию и не ошибиться в своих подсчетах.
Как измерить объем талии?
Для начала стоит отметить, что вам понадобится сантиметровая лента – иначе узнать, какой у вас обхват талии, не удастся.
1. Вам необходимо избавиться от одежды, которая в данный момент на вас – майка или кофта добавляет лишние сантиметры, которые вам вряд ли нужны для точного результата. Вы можете просто приподнять одежду до груди. Стоит спустить еще и брюки, если они слишком с высокой посадкой.
2. Следующий шаг – найти ту самую талию. Она находится между верхней частью бедер и основанием грудной клетки. Это, чаще всего, мягкая зона, а над ней – кости. Талия находится на уровне пупка или чуть выше него.
3. Далее оберните сантиметровую ленту вокруг своей талии. Для этого вам стоит встать прямо и не задерживать дыхание. Начало ленты расположите около пупка. Сантиметр не должен болтаться на теле. Необходимо, чтобы он плотно облегал талию, но при этом не врезался в кожу. Кроме того, обратите внимание, чтобы сантиметровая лента не перекрутилась, например, на спине. В противном случае результат будет не совсем верный.
4. Взгляните на сантиметровую ленту, но перед этим соберитесь с мыслями. Значение, которое вы хотите узнать, будет видно на конце ленты, сомкнувшейся с началом, то есть в районе пупка. Цифра, которую вы увидите, будет означать ваш обхват талии в сантиметрах.
5. Если вы интересуетесь, как правильно измерить талию, стоит запомнить еще одно правило: лучше дважды проверять результат. Выполните такое же измерение еще раз, чтобы точно значит, что значение верное. Если же второй замер отличается от предыдущего, то придется проделать те же операции в третий раз.
Какая талия должна быть у здорового человека?
Известно, что у мужчин талия должна быть меньше 94 сантиметров, а у женщин – меньше 80 сантиметров. Завышенные отметки говорят о том, что у вас могут быть какие-то проблемы со здоровьем или предрасположенность к ним. Среди них, например, инсульт или порок сердца. Слишком большой объем талии может говорить о риске заболеть диабетом второго типа и раком.
В том случае, если вы заметили, что ваша талия больше необходимых показателей, вам нужно обратиться к врачу. Возможно, он назначит вам анализы, а после – пропишет диету и даст рекомендации по занятиям спортом.
Стоит ли переживать из-за размеров талии?
Существуют несколько факторов, которые могут повлиять на размер талии. Так, например, у беременных женщин она заметно увеличивается. Кроме того, на объеме талии сказываются болезни, приводящие к увеличению живота. Слишком большой объем талии характерен, в том числе и для некоторых наций. Например, подобное встречается у китайцев и японцев.
Кстати, если вы хотите активно следить за динамикой уменьшения или увеличения обхвата талии в случае, если вам необходимо похудеть или потолстеть, лучше снимать мерки каждую неделю. Если вы просто планируете наблюдать за своим здоровьем, достаточно будет результатов раз в месяц. И помните, что талию можно скорректировать без каких-либо жестких диет. Достаточно спорта и правильного питания.
Вот и пример упражнения, которое поможет сделать талию тоньше: «вакуум». Оно делается на пустой желудок. Вам необходимо согнуть ноги в коленях, лежа на спине, и сделать глубокий вдох, выдыхая воздух через рот. Но есть важное правило: стоит задержаться на вдохе минимум на 15 секунд, а с каждым днем по чуть-чуть увеличивать продолжительность и доходить в своих начинаниях до минуты. Лучше повторять упражнение от трех до пяти раз подряд каждый день.